chapter 2. Basic Structures: Sets, Functions, Sequences, Sums, and Matrices
2.2 Set Operations
Union 합집합
- 표기: A ∪ B
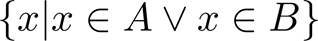
Example: What is {1,2,3} ∪ {3, 4, 5}?
Solution: {1,2,3,4,5}

Intersection 교집합
- 표기: A ∪ B

- 만약 교집합이 존재하지 않는다면, A와 B는 disjoint되었다고 말한다.
Example: What is {1,2,3} ∩ {3,4,5} ?
Solution: {3}
Example: What is {1,2,3} ∩ {4,5,6} ?
Solution: ∅


Complement 여집합
- U - A (전체집합에서 A를 제외한 나머지)
- Ā(or Ac) = {x ∈ U | x ∉ A}
Example: If U is the positive integers less than 100, what is the complement of {x | x > 70}
Solution: {x | x ≤ 70}

Difference 차집합
- A - B (A에서 A와 B의 교집합을 뺀 집합)



The Cardinality of the Union of Two Sets 합집합의 카디널리티
- Inclusion-Exclusion ☞ |A ∪ B| = |A| + |B| + |A ∩ B|
- 두 집합을 더한 후 중복되는 부분(A와 B의 교집합)의 원소 개수를 한 번 빼준다.

Review Questions
Example: U = {0,1,2,3,4,5,6,7,8,9,10}, A = {1,2,3,4,5}, B ={4,5,6,7,8}
1. A ∪ B
Solution: {1,2,3,4,5,6,7,8}
2. A ∩ B
Solution: {4,5}
3. Ā
Solution: {0,6,7,8,9,10}
4. Bc
Solution: {0,1,2,3,9,10}
5. A – B
Solution: {1,2,3}
6. B – A
Solution: {6,7,8}
Set Identities(집합의 항등)
Identity laws(항등 법칙)

Domination laws(지배 법칙)

Idempotent laws(멱등 법칙)
연산을 여러 번 적용하더라도 결과가 달라지지 않는 성질. 예를 들어, 수 1은 곱셈의 멱등원이다: 1 × 1 = 1.

Complementation law(보 법칙)

Commutative laws(교환 법칙)

Associative laws(결합 법칙)

Distributive laws(분배 법칙)

De Morgan’s laws(드모르간 법칙)

Absorption laws(흡수법칙)
바깥과 안쪽 기호가 반대

Complement laws(보수법칙)

Proving Set Identities
집합의 항등을 증명하는 다양한 방법들:
1. 각 집합이 다른 집합의 부분 집합임을 증명한다.
2. set builder 표기법과 명제 논리를 사용한다.
3. 멤버십 테이블(진리표와 비슷): 비교하고자 하는 집합의 조합 요소들의 값이 동일한지 확인한다. 집합에 있음을 나타내기 위해 1을 사용하고 집합에 없음을 나타내기 위해 0을 사용한다.
Proof of Second De Morgan Law 드모르간 두 번째 법칙의 증명

서로가 서로의 부분집합인지 확인하는 방식으로 증명

A ∩ B의 여집합에 원소 x가 존재한다고 가정한다.
A ∩ B의 여집합에 원소 x가 존재하므로 그 여집합인 A ∩ B에는 x가 존재하지 않는다.
x가 A ∩ B의 원소가 아니라는 식으로 표현식을 나타낸다.드모르간 첫번째 법칙을 이용해 괄호의 not을 안으로 넣어준다.해당 표현식을 다시 집합 관련 표현식으로 바꾸어준다.

Set-Builder Notation: Second De Morgan Law ☞ Set-Builder 표기법을 이용한 증명

Membership Table

진리표를 작성하듯이 하나하나 작성해 나간 뒤 최종 결과를 비교한다.
출처:
Discrete Mathematics and Its Applications (K. H. Rosen 저, McGraw Hill, 2007)
위키백과 멱등법칙
'Computer Science > 이산수학' 카테고리의 다른 글
| 이산수학 2.1 Sets 집합 (0) | 2021.09.24 |
|---|---|
| 이산수학 1.4 Predicates and Quantifiers 술어와 한정 기호(3) (0) | 2021.09.24 |
| 이산수학 1.4 Predicates and Quantifiers 술어와 한정 기호(2) (0) | 2021.09.24 |
| 이산수학 1.4 Predicates and Quantifiers 술어와 한정 기호(1) (0) | 2021.09.24 |
| 이산수학 1.3 Propositional Equivalences 명제 동치 (0) | 2021.09.09 |
| 이산수학 1.2 Aplication of Propositional Logic 명제이론의 응용 (0) | 2021.09.08 |

