chapter 1. The Foundations: Logic and Proofs
1.4 Predicates and Quantifiers
Equivalences in Predicate Logic
- predicates(술어)와 quantifiers(한정자)가 포함된 문장은 동일한 진리 값을 갖는 경우에만 논리적으로 동일하다.
- 이 statements(진술)로 대체되는 모든 predicate에 대하여
- 표현식의 변수에 사용되는 담론의 모든 domain에 대해
- 표기법 S ≡ T: S와 T가 논리적으로 동일하다.
- Example: ∀x¬¬S(x) ≡ ∀xS(x)
Thinking about Quantifiers as Conjunctions and Disjunctions
- Conjunctions: ∧
- Disjunctions: ∨
- domain이 유한(finite)하다면, universally quantified proposition는 한정자가 없는 명제의 conjunctions과 동일하며, existentially quantified proposition는 한정자가 없는 명제의 disjunctions과 동일하다.
- U가 정수 1, 2, 3으로 구성된 경우:
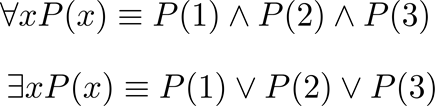
- domain이 무한(infinite)하다고 해도 이러한 방식의 quantifiers를 생각할 수 있지만, quantifiers가 없는 equivalent expressions은 무한히 길 것이다.
Negating Quantified Expressions
[∀xJ(x)]
- ∀xJ(x): "Every student in your class has taken a course in Java."
- 위 명제에서 J(x)는 "x has taken a course in Java"이고, domain은 students in your class이다.
- original statement의 부정: "It is not the case that every student in your class has taken Java." 당신의 클래스 안의 모든 학생들이 Java 수업을 수강한 것은 아니다.
- ☞ "There is a student in your class who has not taken Java." 당신의 클래스 안에 Java 수업을 수강하지 않은 학생이 있다.
- *¬∀xJ(x) ≡ ∃x¬J(x)
*¬∀xJ(x): not all, J(x)가 아닌 것이 존재한다.
[∃xJ(x)]
- ∃xJ(x): There is a student in this class who has taken a course in Java.”
- 위 명제에서 J(x)는 “x has taken a course in Java.”
- original statement의 부정: “It is not the case that there is a student in this class who has taken Java.” 이 반에 자바를 수강한 학생이 있는 것은 아니다.
- ☞ “Every student in this class has not taken Java” 이 class의 모든 학생이 Java를 수강하지 않았습니다.
- ¬∃xJ(x) ≡ *∀x¬J(x)
*∀x¬J(x): 모든 x에 대해 not J(x)
De Morgan’s Laws for Quantifiers
The rules for negating quantifiers are:

The reasoning in the table shows that:
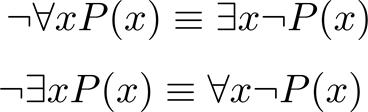
Translation from English to Logic
Examples:
1. “Some student in this class has visited Mexico.”
Solution: Let M(x) denote “x has visited Mexico” and S(x) denote “x is a student in this class,” and U be all people.
∃x (S(x) ∧ M(x))
2. “Every student in this class has visited Canada or Mexico.”
Solution: Add C(x) denoting “x has visited Canada.”
∀x (S(x) → (M(x) ∨ C(x)))
Some Fun with Translating from English into Logical Expressions
U = {fleegles, snurds, thingamabobs}
F(x): x is a fleegle
S(x): x is a snurd
T(x): x is a thingamabob
Translate “Everything is a fleegle”
Solution: ∀x F(x)
U = {fleegles, snurds, thingamabobs}
F(x): x is a fleegle
S(x): x is a snurd
T(x): x is a thingamabob
Translate “Nothing is a snurd.”
Solution: ¬∃x S(x) What is this equivalent to?
Solution: ∀x ¬ S(x)
U = {fleegles, snurds, thingamabobs}
F(x): x is a fleegle
S(x): x is a snurd
T(x): x is a thingamabob
Translate “All fleegles are snurds.”
Solution: ∀x (F(x)→ S(x))
U = {fleegles, snurds, thingamabobs}
F(x): x is a fleegle
S(x): x is a snurd
T(x): x is a thingamabob
Translate “Some fleegles are thingamabobs.”
Solution: ∃x (F(x) ∧ T(x))
U = {fleegles, snurds, thingamabobs}
F(x): x is a fleegle
S(x): x is a snurd
T(x): x is a thingamabob
Translate “No snurd is a thingamabob.”
Solution: ¬∃x (S(x) ∧ T(x)) What is this equivalent to?
Solution: ∀x (¬S(x) ∨ ¬T(x))
U = {fleegles, snurds, thingamabobs}
F(x): x is a fleegle
S(x): x is a snurd
T(x): x is a thingamabob
Translate “If any fleegle is a snurd then it is also a thingamabob.”
Solution: ∀x ((F(x) ∧ S(x))→ T(x))
출처: Discrete Mathematics and Its Applications (K. H. Rosen 저, McGraw Hill, 2007)
'Computer Science > 이산수학' 카테고리의 다른 글
| 이산수학 2.2 Set Operations 집합 연산 (0) | 2021.09.25 |
|---|---|
| 이산수학 2.1 Sets 집합 (0) | 2021.09.24 |
| 이산수학 1.4 Predicates and Quantifiers 술어와 한정 기호(2) (0) | 2021.09.24 |
| 이산수학 1.4 Predicates and Quantifiers 술어와 한정 기호(1) (0) | 2021.09.24 |
| 이산수학 1.3 Propositional Equivalences 명제 동치 (0) | 2021.09.09 |
| 이산수학 1.2 Aplication of Propositional Logic 명제이론의 응용 (0) | 2021.09.08 |

