chapter 2. Basic Structures: Sets, Functions, Sequences, Sums, and Matrices
2.1 Sets 집합
Sets
- 집합은 순서가 없는(unordered) object들의 모임이다.
- ex. 반의 학생들 / 방의 의자들
- 집합의 object들을 elements(원소), 또는 집합의 members(멤버)라 칭한다. 집합은 이러한 element들을 포함(contain)하고 있다.
- a ∈ A : a는 집합 A의 element이다.
- a ∉ A : a는 집합 A의 element가 아니다.
Describing a Set: 원소나열법
- S = {a,b,c,d}
- 순서는 중요하지 않다. ☞ S = {a,b,c,d} = {b,c,a,d}
- 중복 멤버는 허용하지 않는다. ☞ S = {a,b,c,d} = {a,b,c,b,c,d}
- 패턴이 명확할 때 모든 멤버들을 나열하지 않고 생략 가능 ☞ S = {a,b,c,d, ……,z }
Some Important Sets
N = natural numbers = {0,1,2,3….} ☞ 0을 포함하는 자연수의 집합
Z = integers = {…,-3,-2,-1,0,1,2,3,…} ☞ 0을 포함하는 정수의 집합
Z⁺ = positive integers = {1,2,3,…..} ☞ 0을 포함하지 않는 양의 정수의 집합
R = set of real numbers ☞ 0을 포함하는 실수의 집합
R+ = set of positive real numbers ☞ 0을 포함하지 않는 양의 실수의 집합
C = set of complex numbers ☞ 복소수의 집합
Q = set of rational numbers ☞ 유리수의 집합
Set-Builder Notation(조건제시)
- 집합 내의 모든 멤버들이 만족해야 하는 특성을 명시하는 것
ex.
S = {x | x is a positive integer less than 100}
O = {x | x is an odd positive integer less than 10}
O = {x ∈ Z⁺ | x is odd and x < 10} = {x | x ∈ Z⁺ ^ x is odd and x < 10} (위 O와 아래 O는 동일한 집합이다)
- 명제를 사용한 조건제시법: S = {x | P(x)}
- Positive rational numbers 표현: Q+ = {x ∈ R | x = p/q, for some positive integers p,q}
Interval Notation
[a,b] = {x | a ≤ x ≤ b}
[a,b) = {x | a ≤ x < b}
(a,b] = {x | a < x ≤ b}
(a,b) = {x | a < x < b}
닫힌 구간 closed interval [a,b]
열린 구간 open interval (a,b)
Universal Set and Empty Set
universal set
- 전체 집합
- 모든 것을 포함함
- 기호: U
empty set
- 공집합
- 원소가 존재하지 않는 것
- 기호: ∅
Some things to remember
- 집합은 집합의 원소가 될 수 있다. ex. {{1,2,3},a, {b,c}} / {N,Z,Q,R}
- empty set은 empty set을 원소로 포함한 집합과 다르다. ∅ ≠ { ∅ }
Set Equality 집합 동등성
두 집합은 동일한 원소들을 가지고 있을 때 동일하다.

모든 x에 대해, x가 A에 포함되었을 때 x는 B에도 포함된다.
모든 x에 대해, x가 B에 포함되었을 때 x는 A에도 포함된다.
Subsets 부분집합
A의 모든 원소가 B의 원소라면, 집합 A는 B의 부분집합이다.
표기: A ⊆ B

위 식을 만족할 때만 A ⊆ B이 성립한다.
1. Because a ∈ ∅ is always false, ∅ ⊆ S, for every set S.
☞모든 집합 S에 대해 a는 공집합의 원소가 아니고, 공집합은 S의 부분집합이다.
2. Because a ∈ S → a ∈ S, S ⊆ S, for every set S.
☞모든 집합 S에 대해 a가 S의 원소라면, a는 S의 원소이다. S는 S의 부분집합이다.
Showing a Set is or is not a Subset of Another Set 집합이 다른 집합의 부분집합인지 보이기
1. A가 B의 부분집합임을 보이는 법: 원소 x가 A에도 있고 B에도 있음을 보인다.
2. A가 B의 부분집합이 아님을 보이는 법: 집합 A에 포함된 원소 x가 B에 포함되어 있지 않음을 보인다.
Another look at Equality of Sets 집합의 동등을 다르게 바라보기
A = B일 때

이는 아래와 같이 표현 가능하다. (biconditional을 하나씩 쪼갬)

따라서 A = B일 때 A는 B의 부분집합이고 B는 A의 부분집합이다.
Proper Subsets 진부분집합
만약 A ⊆ B이지만 A≠B일 때, A를 B의 진부분 집합이라고 한다.
표기: A ⊂ B

모든 x에 대해 x가 A의 원소라면 X는 B의 원소이고(A ⊂ B) 어떤 x에 대해서 x가 B의 원소이지만 A의 원소는 아니다(A≠B).

Set Cardinality 집합의 크기
- 유한집합: 집합 S이 n개의 서로 다른 원소를 가질 때 S를 유한집합이라고 한다.
- 무한집합: 유한집합이 아닌 집합. 원소의 개수가 유한하지 않은 집합이다.
- 유한집합 A의 cardinality |A|: A의 원소 갯수.(중복 허용x)
Examples:
1.|ø| = 0 (공집합의 cardinality)
2.Let S be the letters of the English alphabet. Then |S| = 26 (알파벳 갯수)
3.|{1,2,3}| = 3
4.|{ø}| = 1 (공집합을 집합으로 가지는 집합의 cardinality)
5.The set of integers is infinite.
Power Sets 멱집합
집합A의 모든 부분집합의 집합
표기: P(A) ☞ A의 멱집합
Example: If A = {a,b} then
P(A) = {ø, {a},{b},{a,b}}
위 예제에서 알 수 있듯이, n개의 원소를 가진 집합의 멱집합의 카디널리티는 2ⁿ이다.
Tuples
- 순서가 있는(ordered) n-tuple(a1,a2,…..,an)은 첫 번째 원소로 a1을, 두 번째 원소로 a2를 갖는 순서 집합이다.
- 해당 원소가 동일한 경우에만 두 개의 n-tuple이 동일하다. (n: 원소의 갯수)
- 2-tuples을 ordered pairs라고 합니다.
- a = c and b = d인 경우에만 ordered pairs (a,b)와 (c,d)가 같다.
Cartesian Product
- 두 개의 집합 A, B에 대해서 a ∈ A and b ∈ B를 만족하는 ordered pairs (a,b)의 집합
- 표기: A × B

Example:
A = {a,b} B = {1,2,3} 2개 X 3개
A × B = {(a,1),(a,2),(a,3), (b,1),(b,2),(b,3)} 6개
- A × B의 부분집합 R을 집합 A에서 집합 B까지의 relation이라 부른다.
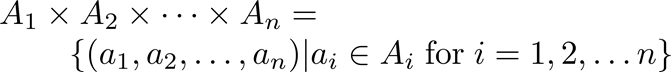
Example: What is A × B × C where A = {0,1}, B = {1,2} and C = {0,1,2}
Solution: A × B × C = {(0,1,0), (0,1,1), (0,1,2),(0,2,0), (0,2,1), (0,2,2),(1,1,0), (1,1,1), (1,1,2), (1,2,0), (1,2,1), (1,1,2)}
출처: Discrete Mathematics and Its Applications (K. H. Rosen 저, McGraw Hill, 2007)
'Computer Science > 이산수학' 카테고리의 다른 글
| 이산수학 2.2 Set Operations 집합 연산 (0) | 2021.09.25 |
|---|---|
| 이산수학 1.4 Predicates and Quantifiers 술어와 한정 기호(3) (0) | 2021.09.24 |
| 이산수학 1.4 Predicates and Quantifiers 술어와 한정 기호(2) (0) | 2021.09.24 |
| 이산수학 1.4 Predicates and Quantifiers 술어와 한정 기호(1) (0) | 2021.09.24 |
| 이산수학 1.3 Propositional Equivalences 명제 동치 (0) | 2021.09.09 |
| 이산수학 1.2 Aplication of Propositional Logic 명제이론의 응용 (0) | 2021.09.08 |

