반응형
문제
https://school.programmers.co.kr/learn/courses/30/lessons/120878
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
🐍파이썬
def solution(a, b):
a_arr = []
b_arr = []
# 1. 기약분수로 나타내기-분자, 분모의 소인수 확인, 동일한 소인수는 제거
i = 2
while a >= i:
if a % i == 0:
a //= i
a_arr.append(i)
else:
i += 1
i = 2
while b >= i:
if b % i == 0:
b //= i
if i in a_arr:
a_arr.remove(i) #약분
else:
b_arr.append(i)
else:
i += 1
#2. 분모의 소인수가 2와 5인지 확인하기
for i in b_arr:
if not i in [2, 5]:
return 2
return 1
다른 풀이 방법
from math import gcd
def solution(a, b):
b //= gcd(a,b)
while b % 2==0:
b //= 2
while b % 5==0:
b //= 5
return 1 if b==1 else 2gcd() 사용. 최대공약수를 이용해 기약분수 상태로 만들 수 있다.
문제풀이에 사용해야 하는 것은 b(분모)뿐이므로 b만 체크해서 2와 5이외의 수가 있는지 찾아낸다. b를 2와 5로 나누어 남는 수가 1이 아니라면 b에 2, 5가 아닌 다른 수가 곱해져 있었다는 뜻이므로 유한소수가 아니다.
def solution(a, b):
answer = 0
for i in range(2, min([a, b]) + 1): #공약수 구해서 a, b에서 나누기(기약분수 만들기)
while a % i == 0 and b % i == 0:
a = a // i
b = b // i
while b % 2 == 0:
b = b // 2
while b % 5 == 0:
b = b // 5
if b == 1:
answer = 1
else:
answer = 2
return answergcd()를 사용하지 않은 코드. 직접 for문을 돌며 a, b를 공약수로 나눠준 부분 외의 로직은 위 코드와 동일하다.
🐥자바스크립트
function solution(a, b) {
// 1. 기약분수 만들기
let gcd = 1;
for(let i = 2; i <= Math.min(a, b); i++){
if(a % i === 0 && b % i === 0){
gcd = i;
}
}
b /= gcd; //공약수로 b 나누기
// 2. 분모에 2, 5 이외의 숫자가 곱해져 있는지 확인
while(b % 2 == 0) { b /= 2 };
while(b % 5 == 0) { b /= 5 };
return b === 1 ? 1 : 2;
}위 파이썬 <다른 풀이 방법>과 GCD 관련 설명한 블로그를 참고해 코드를 작성했다.
다른 풀이 방법
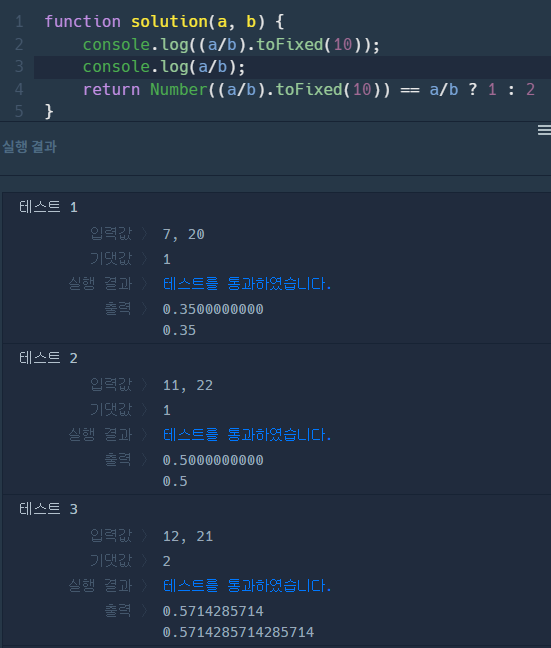
function solution(a, b) {
return Number((a/b).toFixed(10)) == a/b ? 1 : 2
}소수점 아래 숫자가 계속 되는지 아닌지 확인하여 유한소수를 판별하였다. 소수점 아래 숫자가 계속되면 무한소수
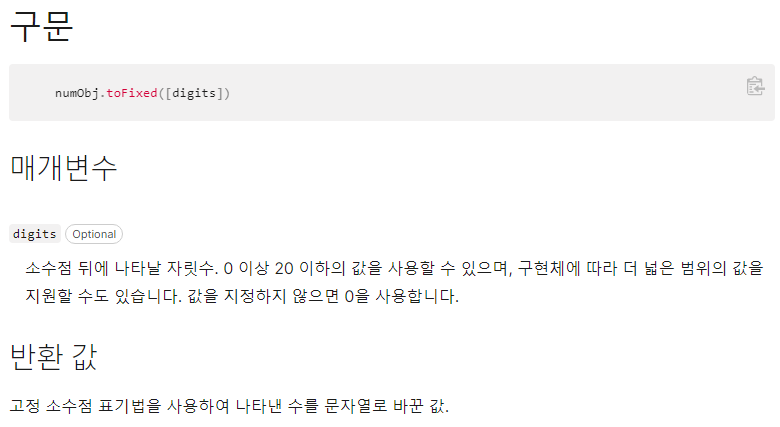
숫자를 고정 소수점 표기법(fixed-point notation)으로 표시하는 메서드, 소수점 아래 N자리까지 표현
반응형
'Problem Solving > 프로그래머스' 카테고리의 다른 글
| [프로그래머스 | 파이썬 / 자바스크립트] [1차] 뉴스 클러스터링(2018 KAKAO BLIND RECRUITMENT/ level 2) (0) | 2023.02.28 |
|---|---|
| [프로그래머스 | 파이썬 / 자바스크립트] 연속 부분 수열 합의 개수(연습문제/ level 2) (0) | 2023.02.28 |
| [프로그래머스 | 파이썬 / 자바스크립트] 이진수 더하기(코딩테스트 입문/ level 0) (0) | 2023.02.28 |
| [프로그래머스 | 파이썬 / 자바스크립트] 대문자와 소문자(코딩테스트 입문/ level 0) (0) | 2023.02.25 |
| [프로그래머스 | 파이썬 / 자바스크립트] 피로도(완전탐색/ level 2) (0) | 2023.02.25 |
| [프로그래머스 | 파이썬 / 자바스크립트] 다항식 더하기(코딩테스트 입문/ level 0) (0) | 2023.02.24 |


